
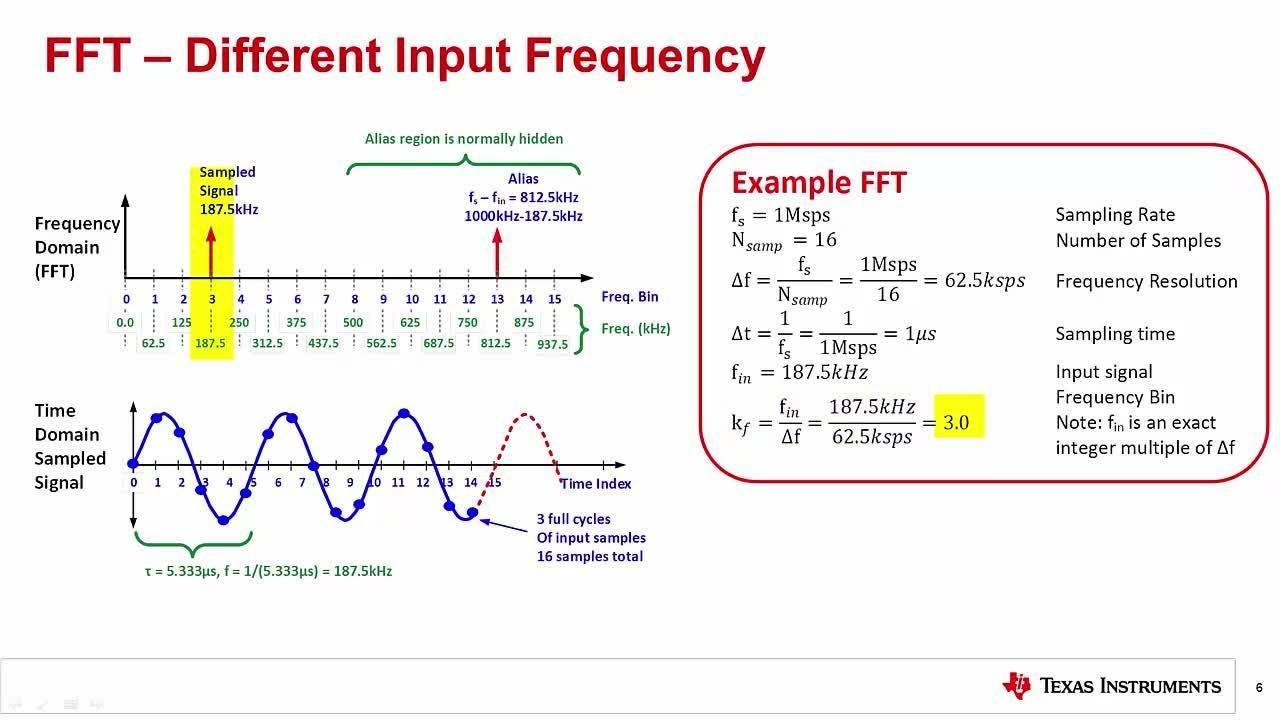
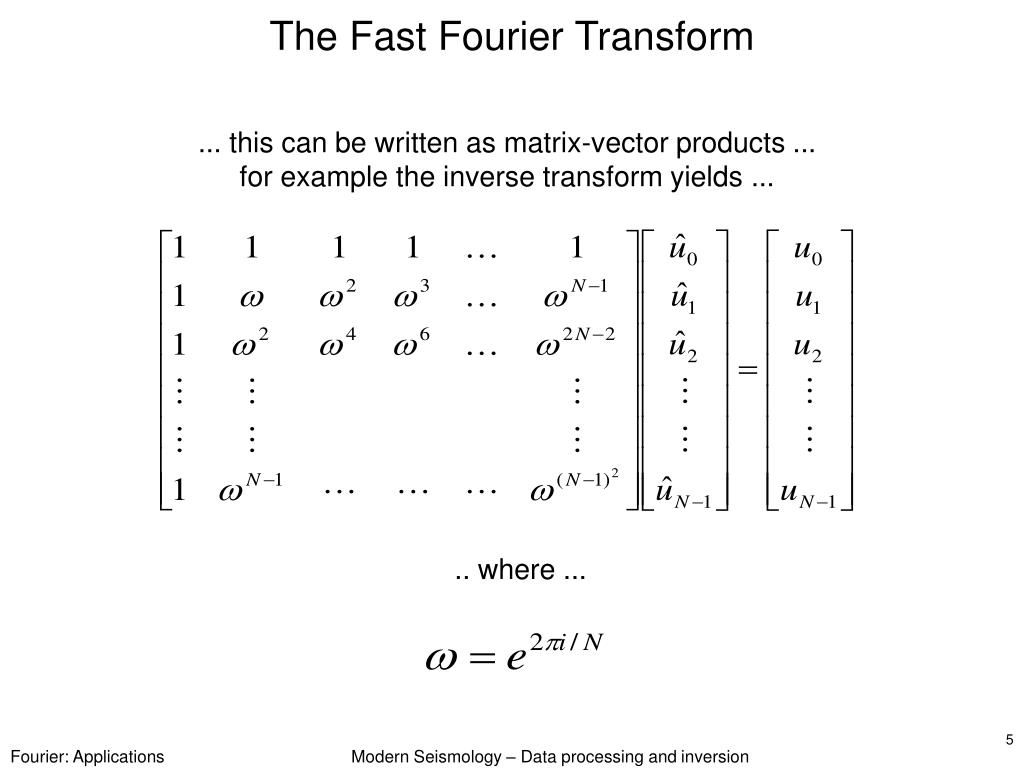
A specific window function should be selected according to the kind of signals being analyzed. Several window functions are supported, including Triangular, Rectangle, Bartlett, Welch, Hanning, Hamming, and Blackman, each of which has its own unique advantages and disadvantages. Origin supports the use of window functions to mitigate leakage. This will cause both the amplitude and position of a frequency measurement to be inaccurate. The terminology fast Fourier transform (FFT) refers to efficient methods for computation of discrete Fourier transforms (DFT). However, if the true signal is not periodic or if the assumed periodic length is not correct, leakage will occur. When the FFT is used, attention should be paid to leakage, which is caused by the FFT's assumption that the input signal repeats periodically and that the periodic length is equal to the length of the actual input. Furthermore, both two-sided and one-sided powers can be computed. The power density estimation can be made by three different methods: MSA, SSA, and TISA. Meanwhile, it can also provide the magnitude, amplitude, phase, power density, and other computation results. The result of the FFT contains the frequency data and the complex transformed result. Note that the input signal of the FFT in Origin can be complex and of any size. By using FFT instead of DFT, the computational complexity can be reduced from O( ) to O( n log n). Let ( ) be a sequence of length N, then its DFT is the sequence ( ) given byĪ fast Fourier transform (FFT) is an efficient way to compute the DFT. A discrete Fourier transform (DFT) converts a signal in the time domain into its counterpart in frequency domain.


 0 kommentar(er)
0 kommentar(er)
